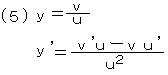|
微分係数は導関数から簡単に求められました。しかし、導関数を求めるのは （＝微分するのは）lim が出てきてめんどうですね。
やって法則を見つけ出したのです。
ｙ＝ｘ２を微分するとｙ’＝２ｘになります。 ※ｙ’は ｙ’の本来の意味を忘れてしまわないように注意して下さい。 ｙ＝ｘ３を微分するとｙ’＝３ｘ２ ｙ＝ｘ４を微分するとｙ’＝４ｘ３
ろんな公式を導きました。もちろん、今では公式の数学的証明もなされていま すので、安心して使うことができます。
ｙ’＝ｎｘｎ−１
ｙ’＝ｋ・ｎｘｎ−１
ｙ’＝ｕ’± ｖ’
ｙ’＝ｕ’ｖ＋ｕｖ’
ｙ’＝ｃｏｓｘ
ｙ’＝−ｓｉｎｘ （マイナスが付きます）
※ｅは微分・積分でよく使われる、自然対数の底です。（関数電卓にもつ いています。）ｅ＝２．７１８２８・・・で、フナヒトハチフタハチ （鮒一鉢二鉢）と覚えましょう。
ｙ’＝ｅｘ （微分しても変わらない、変な関数です。）
こう書いても何のことか解りませんね。 ｙはｔの関数で、またｔはｘの関数の微分です。ややこしいですね。こ のような関数の関数の微分を、りょうかんは缶詰微分（カンヅメ微分） と呼んでいます。 この微分がいちばん難しいですが、つぎの練習問題で勉強すれば、すら すら解けるようになります。
りょうかん：次は微分公式の練習問題です。 それまでに（１）〜（１１）の公式をしっかり覚えておいてください。 四本：わかりました。 山口：先生、（１１）も覚えないといけませんか？ りょうかん：そうですねぇ、これは覚えなくてもいいかもしれませんね。 北迫：あー、良かった。 次回は、微分公式の練習問題です。 これでおわります。 |
と同じです。このように書くと便利ですが、そのうち
